
Bridging the gap between the new methods of teaching math, with traditional and straightforward approaches.
Here is a perfect example of "new math" vs. "old math":

We also include:
- "NEW MATH" translation guide for parents!
The REASON for this "new math" is to help students learn to solve math problems, (which require more effort and energy right now)—so they can transition to advanced mathematics, easier.
But, if math is already hard for them, the "new math" can be overwhelming. So, we bridge the gap between "new math" and the traditional, logical math, by using real world examples, logic, and easy to remember terminology.
Our math problems include kid friendly humor and silliness, for younger students. And we supply a logical approach for our high school students, with a lot of helpful hints and reminders to help with memorizing facts. We also include help with note taking!
Math subjects we teach:
- Addition & Subtraction
- Telling Time
- Counting Money
- Times Tables / Multiplication
- Math - for middle school
- Pre-Algebra
- Algebra
- Geometry
PLUS!
- "NEW MATH" translation guide for parents!
- Math Test Survival Guide-for students
- Help with study skills and note taking
- Helpful tips for test anxiety
- How to stay focused
- Uncover your learning style quiz!
Plus: *new* math translation guide for parents!
- Addition & Subtraction
- Fact Families
- Place Value
- Expanded Form for addition and subtraction
- Regrouping (carrying)
- Subtracting with ungrouping (borrowing)
Math
Middle School
PLUS!
- Find out your learning style!
- Tips for when students get confused with math during class
- Helpful tip on test anxiety
- Tips for students who avoid math or claim *boredom* with math
- Factors and Multiples
- Fractions
- Decimals
- Percents
- Word Problems
- Ratio
- Rates
- Proportions
- Unit Conversions
- Solving for x
- Solving for x in word problems

Pre-Algebra
PLUS!
Intro into exponents
Math test survival guide!
- Adding and subtracting integers
- Associative and commutative properties
- Multiplying and dividing integers and negative numbers
- Absolute Value
- Mean, median, mode
- Fun quiz about handling stress
- Variables
- Combining like terms
- Distributive property
- Using variables to translate word problems
- Including brain breaks: 20 ways to beat stress
- Solving for x
- Equations
- Word problems
- Solving and graphing inequalities
Geometry

PLUS!
- Memorizing terms made easy!
- Basics
- Working with diagrams
- Intro to proofs
- Triangles, congruence and proofs
- Parallel lines and polygons
- Quadrilaterals
- Brain break: self esteem booster!
- Similarity, circles, area, volume
- Arcs and arc length
- Perimeter and area
- Surface area and volume
- The trouble shooting guide
- List of rules (Theorems and postulates)
Other areas we tutor:
- Algebra
- Learning Multiplication Facts
- Long division
- Telling time
- Counting money
Why "new math"?
The old New Math
When the Soviets launched Sputnik in 1957, the United States went into panic mode. Our schools needed to emphasize math and science so that we wouldn’t fall behind the Soviet Union and its allegedly superior scientists. In 1958, President Eisenhower signed the National Defense Education Act, which poured money into the American education system at all levels.
One result of this was the so-called New Math, which focused more on conceptual understanding of mathematics over rote memorization of arithmetic. Set theory took a central role, forcing students to think of numbers as sets of objects rather than abstract symbols to be manipulated. This is actually how numbers are constructed logically in an advanced undergraduate mathematics course on real analysis, but it may not necessarily be the best way to communicate ideas like addition to schoolchildren. Arithmetic using number bases other than 10 also entered the scene. This was famously spoofed by Tom Lehrer in his song “New Math.”
I attended elementary school in the 1970s, so I missed New Math’s implementation, and it was largely gone by the time I got started. But the way Lehrer tries to explain how subtraction “used to be done” made no sense to me at first (I did figure it out after a minute). In fact, the New Math method he ridicules is how children of my generation – and many of the Common Core-protesting parents of today – learned to do it, even if some of us don’t really understand what the whole borrowing thing is conceptually. Clearly some of the New Math ideas took root, and math education is better for it. For example, given the ubiquity of computers in modern life, it’s useful for today’s students to learn to do binary arithmetic – adding and subtracting numbers in base 2 just as a computer does.
The New Math fell into disfavor mostly because of complaints from parents and teachers. Parents were unhappy because they couldn’t understand their children’s homework. Teachers objected because they were often unprepared to instruct their students in the new methods. In short, it was the implementation of these new concepts that led to the failure, more than the curriculum itself.

Those who ignore history…
In 1983, President Reagan’s National Commission on Excellence in Education released its report, A Nation at Risk, which asserted that American schools were “failing” and suggested various measures to right the ship. Since then, American schoolchildren and their teachers have been bombarded with various reform initiatives, privatization efforts have been launched and charter schools established.
Whether or not the nation’s public schools are actually failing is a matter of serious debate; indeed, many of the claims made in A Nation at Risk were debunked by statisticians at Sandia National Laboratories a few years after the report’s release. But the general notion that our public schools are “bad” persists, especially among politicians and business groups.
Enter Common Core. Launched in 2009 by a consortium of states, the idea sounds reasonable enough – public school learning objectives should be more uniform nationally. That is, what students learn in math or reading at each grade level should not vary state by state. That way, colleges and employers will know what high school graduates have been taught, and it will be easier to compare students from across the country.
The guidelines are just that. There is no set curriculum attached to them; they are merely a list of concepts that students should be expected to master at each grade level. For example, here are the standards in Grade 3 for Number and Operations in Base Ten:
- Use place value understanding and properties of operations to perform multi-digit arithmetic.
- CCSS.Math.Content.3.NBT.A.1 Use place value understanding to round whole numbers to the nearest 10 or 100.
- CCSS.Math.Content.3.NBT.A.2 Fluently add and subtract within 1,000 using strategies and algorithms based on place value, properties of operations, and/or the relationship between addition and subtraction.
- CCSS.Math.Content.3.NBT.A.3 Multiply one-digit whole numbers by multiples of 10 in the range 10-90 (eg, 9 × 80, 5 × 60) using strategies based on place value and properties of operations.
There is a footnote that “a range of algorithms may be used” to help students complete these tasks. In other words, teachers can explain various methods to actually accomplish the mathematical task at hand. There is nothing controversial about these topics, and indeed it’s not controversial that they’re things that students should be able to do at that age.
However, some of the new methods being taught for doing arithmetic have caused confusion for parents, causing them to take to social media in frustration. Take the 32 - 12 problem, for example:
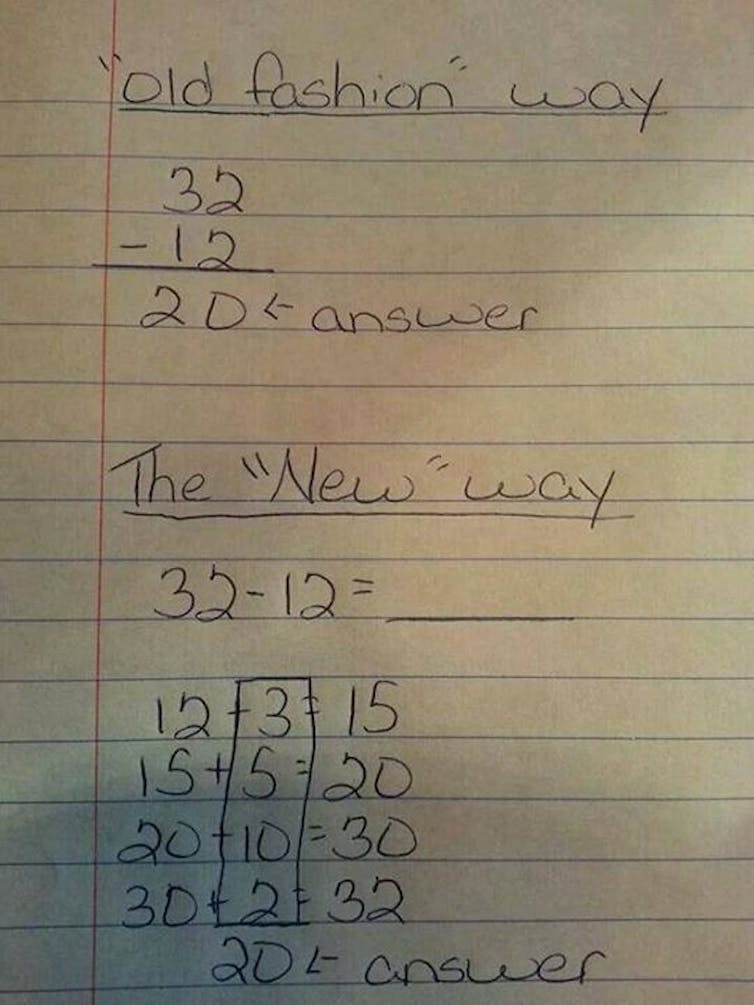
Once again, it’s the implementation that’s causing the problem. Most parents (people age 30-45, mostly), remembering the math books of our youth filled with pages of exercises like this, immediately jump to the “Old Fashion” (sic) algorithm shown. The stuff at the bottom looks like gibberish, and given many adults’ tendency toward math phobia/anxiety, they immediately throw up their hands and claim this is nonsense.
Except that it isn’t. In fact, we all do arithmetic like this in our heads all the time. Say you are buying a scone at a bakery for breakfast and the total price is US$2.60. You hand the cashier a $10 bill. How much change do you get? Now, you do not perform the standard algorithm in your head. You first note that you’d need another 40 cents to get to the next dollar, making $3, and then you’d need $7 to get up to $10, so your change is $7.40. That’s all that’s going on at the bottom of the page in the picture above. Your children can’t explain this to you because they don’t know that you weren’t taught this explicitly, and your child’s teacher can’t send home a primer for you either.

Better intuition about math, better problem-solving
As an instructor of college-level mathematics, I view this focus on conceptual understanding and multiple strategies for solving problems as a welcome change. Doing things this way can help build intuition about the size of answers and help with estimation. College students can compute answers to homework problems to 10 decimal places, but ask them to ballpark something without a calculator and I get blank stares. Ditto for conceptual understanding – for instance, students can evaluate integrals with relative ease, but building one as a limit of Riemann sums to solve an actual problem is often beyond their reach.
This is frustrating because I know that my colleagues and I focus on these notions when we introduce these topics, but they fade quickly from students’ knowledge base as they shift their attention to solving problems for exams. And, to be fair, since the K-12 math curriculum is chopped up into discrete chunks of individual topics for ease of standardized testing assessment, it’s often difficult for students to develop the problem-solving abilities they need for success in higher-level math, science and engineering work. Emphasizing more conceptual understanding at an early age will hopefully lead to better problem-solving skills later. At least that’s the rationale behind the standards.
Alas, Common Core is in danger of being abandoned. Some states have already dropped the standards (Indiana and South Carolina, for example), looking to replace them with something else. But these actions are largely a result of mistaken conflations: that the standards represent a federal imposition of curriculum on local schools, that the standardized tests used to evaluate students are the Common Core rather than a separate initiative.
As the 2016 presidential campaign heats up, support for the Common Core has become a political liability, possibly killing it before it really has a chance. That would be a shame. The standards themselves are fine, and before we throw the baby out with the bathwater, perhaps we should consider efforts to implement them properly. To give the Common Core a fair shot, we need appropriate professional development for teachers and a more phased introduction of new standardized testing attached to the standards.
But, if we do ultimately give in to panic and misinformation, let’s hope any replacement provides proper coherence and rigor. Above all, our children should develop solid mathematical skills that will help them see the beauty and utility of this wonderful subject.
https://www.understood.org/en/school-learning/learning-at-home/homework-study-skills/9-new-math-problems-and-methods
Are you confused by unfamiliar-looking math problems in your child’s homework? The approach to teaching math has changed in recent years. The examples below, created with the help of math specialist Heidi Cohen, can help you help your child with “new math.”
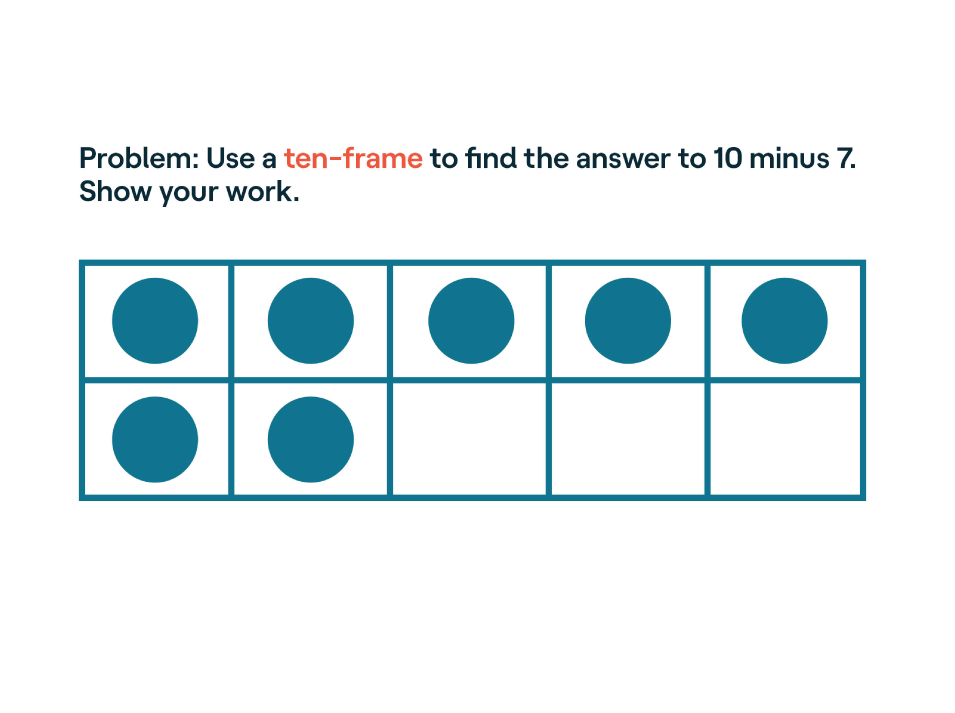
Ten-Frame
A ten-frame is a set of 10 boxes with dots in some or all of the boxes. Kids can see how different combinations of numbers add up to 10. The ten-frame is especially good for showing how subtraction works.

Number Bond
A number bond uses lines to link a group of numbers together, showing how they are related. In the first drawing, the relationship between the numbers 3 and 10 is shown by adding the number 7 to the empty circle (3 + 7 = 10). This helps kids see how a single number can be broken down into smaller parts.
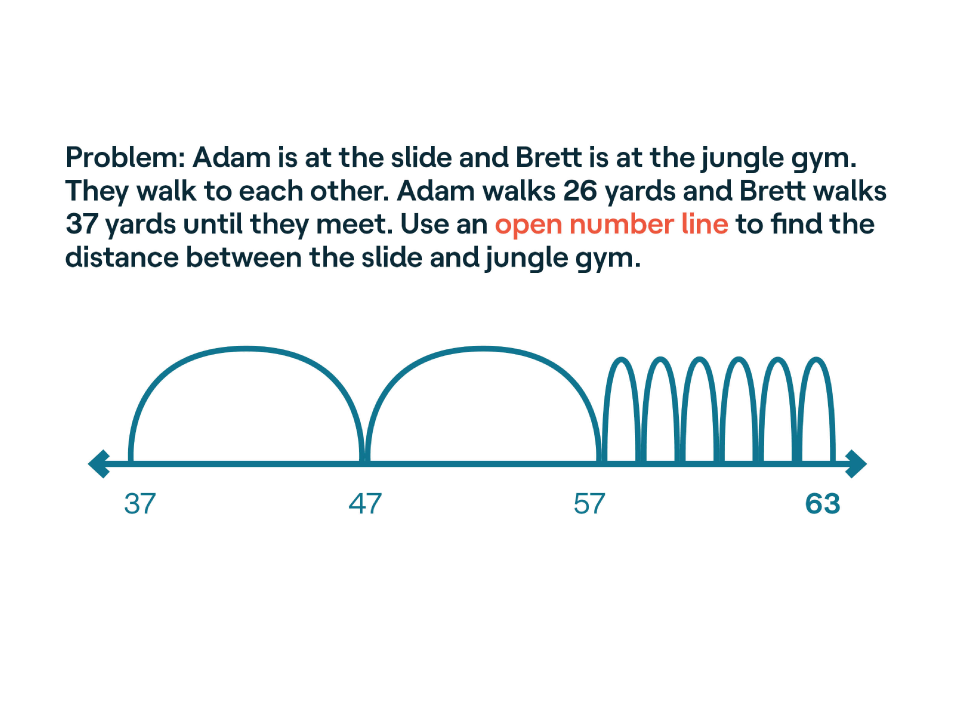
Open Number Line
An open number line has no numbers already written in. The student can use any number as the starting place. (Here, 37 is the starting place because that is how many yards Brett walked. The 26 yards that Adam walked are then added.) The open number line lets kids add or subtract in a visual way. It is often used to help solve word problems.

Decomposing (also called “expanded form”)
Decomposing is a strategy to solve math problems by breaking a number down into its digit values. For example, 37 becomes 30 and 7. Once you break the number down, you can add or subtract the individual digit values to get the answer.

Base Ten
Base ten is a strategy to solve addition and subtraction problems by using a table divided into hundreds, tens, and ones. You’ll probably see the term “regrouping” used for this method. Each number goes into the chart according to its place value. For example, 43 would mean 4 tens and 3 ones. This helps kids see when to “borrow” and “carry” numbers from one place value to another.
Box Multiplication
Box multiplication is a method of breaking numbers down into digit values. In a table, the numbers are broken down by value and multiplied separately. After each number has been multiplied, the total values are added together. This method can be helpful for kids who have trouble with traditional multiplication using larger numbers.
Area Model
An area model uses the length and width of a rectangle or square to break down a multiplication problem. Each shape is calculated and the answers are added together. It’s another way to make math more visual for kids.
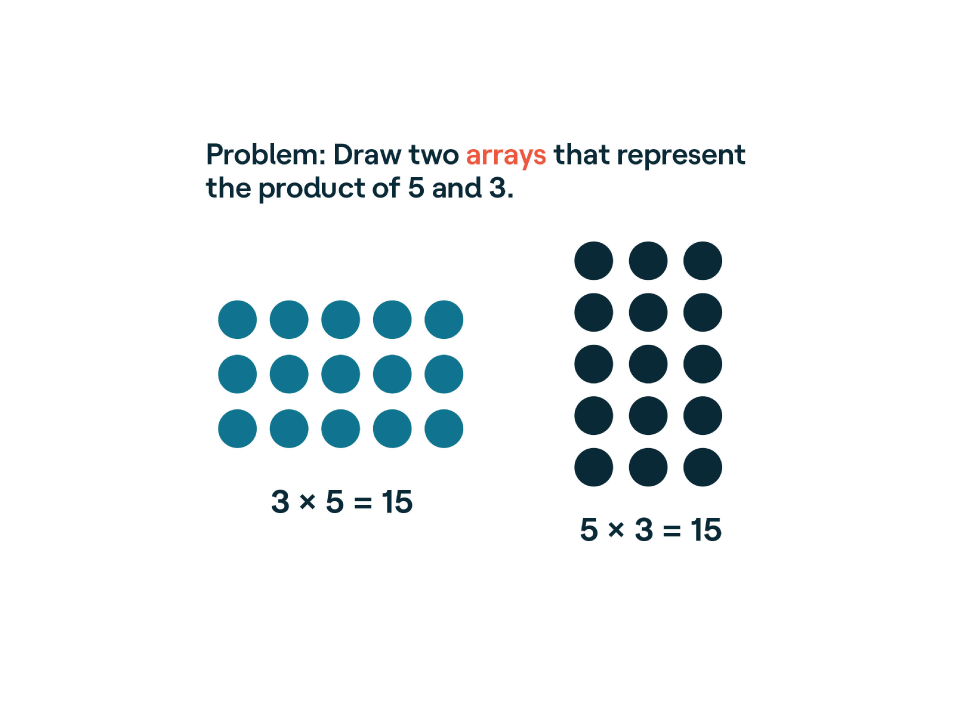
Array
Like an area model, an array is an arrangement of objects that represent a number. This model is often used to help kids see the different qualities of addition and multiplication.
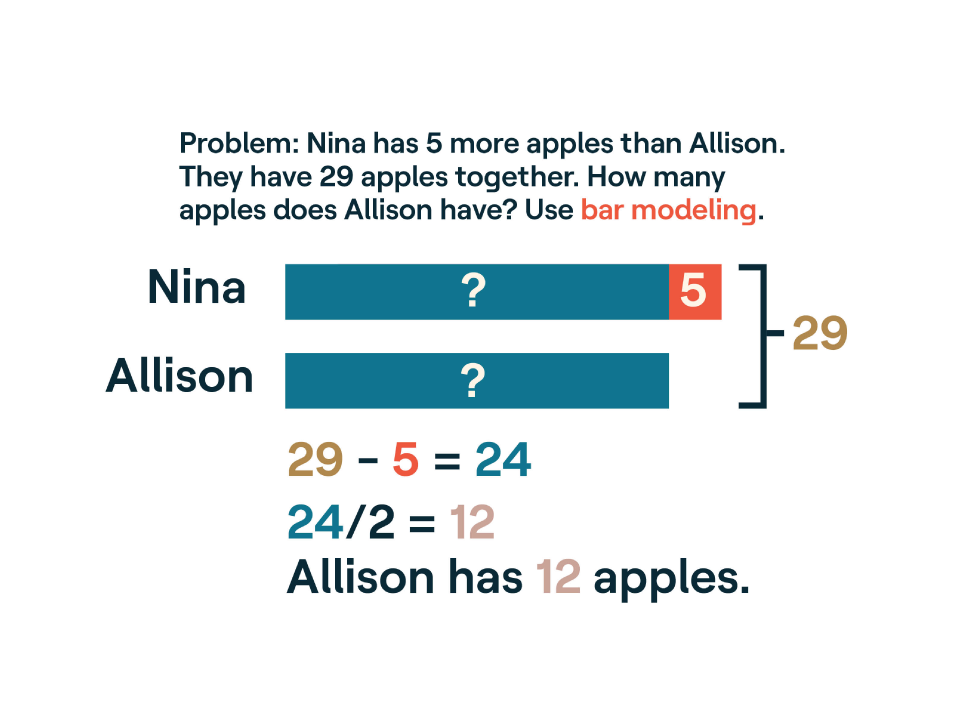
Bar Modeling (also known as a “tape diagram”)
A bar model uses bars to visually represent numbers and unknowns in a word problem. It can help kids see how quantities compare to each other. Kids can adapt a bar model to solve many kinds of problems.